Nama : Nabila Nurul Alifah
Kelas : X MIPA 1
Absen : 17
LUAS SEGITIGA DENGAN TRIGONOMETRI, ATURAN SINUS DAN ATURAN COSINUS
LUAS SEGITIGA DENGAN TRIGONOMETRI
Sebagaimana telah kita pelajari bahwa luas suatu segitiga dapat diperoleh dengan mengalikan alas dan tinggi dari segitiga tersebut dan kemudian membaginya dengan 2, atau dapat dituliskan sebagai

Selain menggunakan rumus di atas, luas segitiga tersebut juga dapat diperoleh dengan menggunakan rumus aturan trigonometri. Untuk penjelasannya, amatilah segitiga ABC berikut!

Gambar 1. Segitiga ABC dengan sudut dan sisi-sisinya
Perhatikan bahwa segitiga ABC pada Gambar 1 terbagi lagi menjadi dua segitiga yakni ΔADC dan ΔBDC. Pada ΔADC, kita peroleh

Dengan demikian,
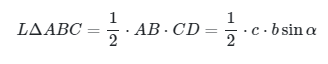
Jadi, luas LΔABC dapat dinyatakan sebagai

Dengan cara yang sama, untuk setiap segitiga ABC juga berlaku:
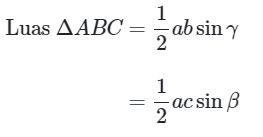
Contoh 1:
Tentukan luas segitiga ABC pada Gambar 1 di atas jika diketahui sisi BC=4 cm, AC=7√3 cm dan ∠C=600.
Pembahasan:
Diketahui BC=a=4 cm; AC=b=7√3 dan ∠C=600. Dengan demikian, kita peroleh

Contoh 2:
Sebuah segitiga ABC diketahui luasnya 18 cm2. Jika panjang sisi BC=4 cm dan AB=6√3 cm, maka tentukanlah besar sudut B.
Pembahasan:
Diketahui luas segitiga = 18, BC=a=4; dan AB=c=6√3. Dengan demikian, kita peroleh

ATURAN SINUS DAN ATURAN COSINUS
Terdapat aturan sinus yang perlu diketahui agar memudahkan penghitungan. Berikut rumusnya:
a / Sin A = b / Sin B = c / Sin C
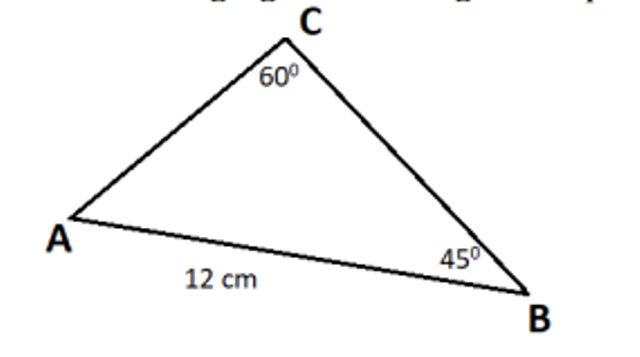
Diketahui segitiga sembarang ABC seperti gambar di bawah ini:
Jika panjang sisi AB = c = 12 cm, dan sisi AC = b cm, diperoleh:
b / Sin B = c / Sin C
b / Sin 45 derajat= 12/Sin 60 derajat
b = 12 Sin 45 derajat / Sin 60 derajat = 12 . 1/2 . √2 dibagi 1/2 √3 = 12√2 / √3
Maka bentuk di atas akan menjadi:
𝑏 = 12√2 / √3 = 12√2 √3 / √3 √3 = 12√6 / 3 = 4√6
Maka, panjang AC = b = 4√6 cm
Aturan cosinus adalah salah satu aturan dalam trigonometri. Aturan ini menjelaskan hubungan antara kuadrat panjang sisi dengan nilai kosinus dari salah satu sudut dalam sebuah segitiga.
Aturan kosinus digunakan untuk menentukan besar salah satu sudut segitiga saat tiga sisi segitiga diketahui. Selain itu, aturan ini dapat digunakan untuk menentukan salah satu sisi segitiga saat diketahui dua sisi dan sudut apitnya.
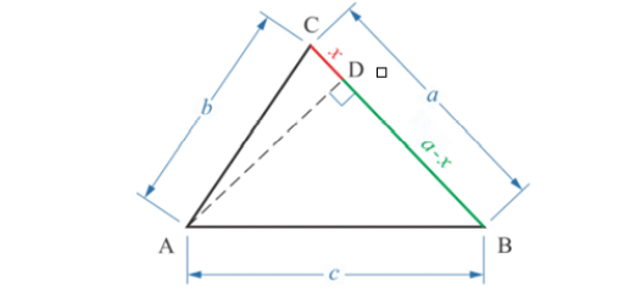
Misalkan panjang AB = c cm; BC = a cm; dan AC = b cm. Jika panjang CD = x cm, panjang BD = (a – x) cm.
Persamaan aturan kosinus ialah 𝑐 2 = 𝑎 2 + 𝑏 2 − 2𝑎𝑏 𝐶𝑜𝑠 𝐶
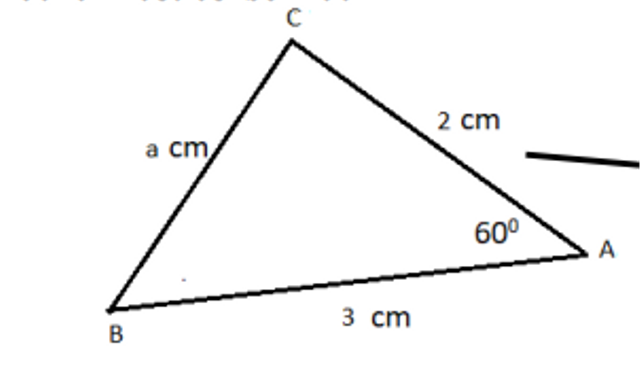
Diketahui segitiga ABC dengan panjang b = 2 cm; c = 3 cm; dan sudut A = 600. Tentukan panjang sisi a?
Dengan menggunakan Aturan Cosinus, maka diperoleh:
𝑎 2 = 2 2 + 3 2 − 2.2.3. 𝐶𝑜𝑠 60 derajat
𝑎 2 = 4 + 9 − 2.2.3. 1 / 2
𝑎 2 = 13 − 6 Maka a = √7
DAFTAR PUSTAKA
https://kumparan.com/kabar-harian/aturan-sinus-dan-cosinus-dalam-sudut-istimewa-trigonometri-1wno1esnnvY/full
https://jagostat.com/matematika-dasar/luas-segitiga-dengan-aturan-trigonometri





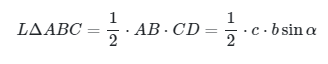

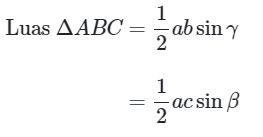


Komentar
Posting Komentar