Nama : Nabila Nurul Alifah
Kelas : X MIPA 1
Absen : 17
KOMPOSISI FUNGSI DAN INVERS FUNGSI
Pengertian Fungsi Komposisi
Fungsi komposisi yaitu penggabungan operasi pada dua jenis fungsi f(x) dan g(x) hingga menghasilkan fungsi baru. Operasi fungsi komposisi biasa yaitu dilambangkan dengan “o” dan dibaca dengan komposisi atau bundaran.
Fungsi baru yang bisa terbentuk dari f (x) dan g (x) yaitu:
(fog) (x) = g dimasukkan ke f
(gof) (x) = f dimasukkan ke g
Fungsi tunggal itu merupakan fungsi yang bisa dilambangkan dengan huruf "kabut" atau juga bisa dibaca dengan "fungsi f bundaran g". Fungsi “fog” yaitu fungsi g yang dilakukan terlebih dahulu, lalu f. Sedangkan untuk fungsi “gof” dibaca dengan fungsi g bundaran f. Maka, “gof” yaitu fungsi f terlebih dahulu, lalu g.
Rumus Fungsi Komposisi

Dari rumus tersebut, definisi yang di dapat menyatakan:
Jika f : A → B ditentukan rumus y = f (x)
Jika g : B → C ditentukan rumus y = g (x)
Jadi, hasil fungsi g dan f:
h (x) = ( g o f ) (x) = g ( f (x))
Dari penjelasan tersebut bisa dikatakan bahwa fungsi yang melibatkan fungsi f dan g bisa ditulis:
(gof) (x) = g (f (x) )
Contoh Soal 1
Diberikan dua buah fungsi yang masing-masing f (x) dan g (x) berturut-turut yaitu:
f (x) = 3x + 2 dan g (x) = 2 - x
Tentukanlah:
a) ( f o g ) (x) &
b) ( g o f ) (x)
Data Jawaban :
f (x) = 3x + 2
g (x) = 2 - x
a) ( f o g ) (x)
“Masukkanlah g (x) nya ke f (x)”
hingga menjadi:
( f o g ) (x) = f ( g (x))
= f (2 - x)
= 3 (2 - x) + 2
= 6 - 3x + 2
= - 3x + 8
b) ( g o f ) (x)
“Masukkanlah f (x) nya ke g (x)”
Hingga menjadi:
( f o g ) (x) = g ( f (x))
= g (3x + 2)
= 2 - (3x + 2)
= 2 - 3x - 2
= - 3x
Contoh Soal 2
Diketahui fungsi f (x) = 3x - 1 dan g (x) = 2x2 + 3. Nilai dari komposisi fungsi ( g o f ) (1) =….?
A. 12
B. 8
C. 7
D. 11
E. 9
Jawaban
Diketahui:
f (x) = 3x - 1 dan g (x) = 2x2 + 3
( g o f ) (1) =…?
Masukkanlah f (x) nya pada g (x) lalu isi dengan 1
( g o f ) (x) = 2(3 x - 1)2 + 3
( g o f ) (x) = 2 ( 9x2 - 6x + 1) + 3
( g o f ) (x) = 18x2 - 12x + 2 + 3
( g o f ) (x) = 18x2 - 12x + 5
( g o f ) (1) = 18(1)2 - 12 (1) + 5 = 11
Contoh Soal 3
Diberi dua buah fungsi:
f (x) = 2x - 3
g (x) = x2 + 2x + 3
Jika (fog) (a) adalah 33, tentukanlah nilai dari 5a
Jawaban:
Cari terlebih dahulu (fog) (x)
(fog) (x) = 2 (x2 + 2x + 3) - 3
(fog) (x) = 2 x2 + 4x + 6 - 3
(fog) (x ) = 2 x2 + 4x + 3
33 sama dengan 2a2 + 4a + 3
2a2 + 4a + 3 = 33
2a2 + 4a - 30 = 0
a2 + 2a - 15 = 0
Faktorkan:
(a + 5) (a - 3) = 0
a = - 5 atau a = 3
Hingga
5a = 5 (−5) = −25 atau 5a = 5 (3) = 15
Fungsi Invers
Suatu fungsi f memiliki fungsi invers (kebalikan) f−1 jika f merupakan fungsi satu-satu dan fungsi pada (bijektif). Hubungan tersebut dapat dinyatakan sebagai berikut:
(f−1)−1=f
Sederhananya, fungsi bijektif berlangsung pada saat jumlah anggota domain sama dengan jumlah anggota kodomain.
Misalkan f fungsi yang memetakan x ke y, sehingga dapat ditulis y = f(x), maka f−1 adalah fungsi yang memetakan y ke x, ditulis x =f−1(y). Sebagai contoh f : A→B fungsi bijektif. Invers dari fungsi f adalah fungsi yang mengawankan setiap elemen B dengan tepat satu elemen pada A. Invers dari fungsi f dinyatakan dengan f−1 seperti di bawah ini:

Terdapat tiga langkah untuk menentukan invers dari suatu fungsi, yaitu:
1. Ubahlah bentuk y = f(x) menjadi bentuk x = f(y).
2. Tuliskan x sebagai f−1 (y) sehingga f−1 (y) = f(y).
3. Ubahlah variabel y dengan x sehingga diperoleh rumus fungsi invers (f−1) (x).
Misalkan, diketahui f(x)=2x+8. Akan dicari fungsi inversnya
1. y = 2x + 8 ↔ x = y−82
2. x = y−82 ↔ (f−1)(y) = y−82
3. f−1(y) = y−82 ↔ f−1 (x) = x−82
Dalam fungsi invers ada rumus khusus seperti berikut ini
Contoh Soal Fungsi Invers
Diketahui  , tentukan
, tentukan  .
.
Pembahasan
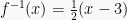
360p geselecteerd als afspeelkwaliteit

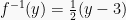
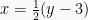

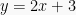
Maka,
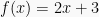
Contoh 2
Diketahui f: R→R dan g: R→R ditentukan oleh f(x) = 2x–7 dan g(x) = 3x+2.
Tentukan (gof)−1(x)
Penyelesaian
CONTOH SOAL 3
Jika diketahui f(x) = 3x−2, tentukan invers dari f(x)
Penyelesaian:
D. Hubungan Sifat Fungsi Invers Dengan Fungsi Komposisi
Berikut adalah hubungan antara fungsi komposisi dan fungsi invers.
(f∘f−1) = (f∘f−1)(x) = I (x)
(f∘g)−1(x) = (g−1∘f−1) (x)
(f∘g)(x)=h(x)→f(x)=(h∘g−1)(x)
Contoh Soal Fungsi Komposisi Fungsi Invers
Misalkan  untuk
untuk 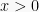 dan
dan  untuk
untuk 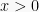 . Jika
. Jika 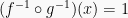 , tentukan nilai (x)
, tentukan nilai (x) .
.
Pembahasan
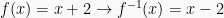
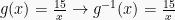
Maka,
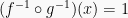
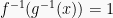
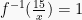


DAFTAR PUSTAKA
http://www.mtkrahma.my.id/2018/10/komposisi-fungsi-fungsi-invers.html
https://blog.teman-belajar.com/fungsi-invers-dan-fungsi-komposisi/
https://www.studiobelajar.com/relasi-fungsi-komposisi-invers/

, tentukan
.
untuk
dan
untuk
. Jika
, tentukan nilai (x)
.





Komentar
Posting Komentar